红黑树

发表于 更新于 分类于
操作系统红黑树相关知识与源码分析

红黑树

红黑树特点

红黑树和别的树的优势在于：

  • 首先它是一个二叉树，这意味着二叉树的插入，查找和删除的平均复杂度在最快情况下都是O(logN)，因此在频繁插入删除和查找的情况下效率非常高。
  • 那为什么不采用二叉搜索树呢，这是因为二叉搜索树在插入的时候可能会导致树变成链表（比如按顺序插入从小到大的结点，一直插入到右子树），这样查找的效率就变成O(N)了。
  • 既然二叉搜索树太弱了，那为什么不用二叉平衡树呢，即AVL。这是因为二叉平衡树需要左右子树高度差<=1, 而红黑树允许左右子树高度差大于1，只是限定了路径上黑色结点数目相同，并且不存在连续的红色结点（最长路径为最短路径的两倍，最长路径是红黑交替的，最短路径为全黑的）。这样通过放宽平衡条件可以换取更少的旋转操作，更少的旋转操作意味着在频繁插入删除的场景下比AVL更高效。

总的来说，红黑树具备以下特点

  • 它是一棵二叉搜索树
  • 每一个节点都会被着色，不是黑色就是红色
  • 根节点必须为黑色
  • 对于一个红色节点，它的孩子或为空，或是黑色。也就是说路径上不能有连续红色节点
  • 从根节点到NULL节点的所有路径上，黑色节点的数量都相同

Linux中红黑树的实现

OK有了以上直观的观念后，咱们来看看Linux中实现红黑树的源码。

首先是红黑树的定义（Linux 6.11版本）, 在内核文件include/linux/rbtree_types.h中，可以看到其实就是一个传统的数据结构，三个指针，分别指向父节点，两个左右子树，但是这个父节点这个值（__rb_parent_color）做了一个优化，具体看注释：

1
2
3
4
5
6
7
8
9
10
struct rb_node {
	unsigned long  __rb_parent_color; //父节点地址&0b00, 这是因为父节点的指针都是8字节对齐的（即后面代码所示__attribute__((aligned(sizeof(long))));），所以低位肯定是0，那么就用低位来存储对应当前节点的颜色即可。
	struct rb_node *rb_right; //右子树
	struct rb_node *rb_left;  //左子树
} __attribute__((aligned(sizeof(long))));
/* The alignment might seem pointless, but allegedly CRIS needs it */

struct rb_root {
	struct rb_node *rb_node;
};

有了数据结构定义之后，我们再来看看相关的一些宏定义用来操作这个数据结构的。主要代码在文件在include/linux/rbtree.h中

1
2
3
4
5
6
7
8
9
10
11
12
// include/linux/rbtree.h
#define rb_parent(r)   ((struct rb_node *)((r)->__rb_parent_color & ~3)) //这里就是获取到parent的指针，把__rb_parent_color成员的低位置0。

#define	rb_entry(ptr, type, member) container_of(ptr, type, member) //

#define RB_EMPTY_ROOT(root)  (READ_ONCE((root)->rb_node) == NULL) //判断root是不是空

/* 'empty' nodes are nodes that are known not to be inserted in an rbtree */
#define RB_EMPTY_NODE(node)  \
	((node)->__rb_parent_color == (unsigned long)(node)) //判断RBnode的父节点是不是自己
#define RB_CLEAR_NODE(node)  \
	((node)->__rb_parent_color = (unsigned long)(node))

然后再来看看第二个比较重要的宏定义 contain_of, 这是因为Linux的数据结构，例如链表和红黑树，都是嵌入到结构体里面的，因此指针指向的也是rb_node结构，并不是包含该rbnode的结构体(例如mm_struct)，要提取真实的mm_struct结构体，则需要使用类似这种container_of宏。

1
2
3
4
5
6
7
8
9
10
// include/linux/container_of.h
#define container_of(ptr, type, member) ({				\
	void *__mptr = (void *)(ptr);					\ //把ptr指针强转成void*， 防止类型警告。
	static_assert(__same_type(*(ptr), ((type *)0)->member) ||	\ //__same_type  GCC内置宏，确保*(ptr)和((type *)0)->member类型相同，这里用了一个技巧写法，即假设0是(type *)类型的指针，从而取其member成员。
		      __same_type(*(ptr), void),			\  //允许 ptr是 void*（某些特殊情况，如 list_head可能是 void*）。
		      "pointer type mismatch in container_of()");	\  //编译时检查
	((type *)(__mptr - offsetof(type, member))); }) // offsetof(type, member)：计算 member在 type结构体中的偏移量（字节）。然后把当前的rbnode减去偏移就是真实的
        
// include/linux/stddef.h        
#define offsetof(TYPE, MEMBER)	__builtin_offsetof(TYPE, MEMBER) // GCC函数，

假设有一个结构体

1
2
3
4
5
struct person {
    int age;
    char name[20];
    struct rb_node rb;  // 假设这是一个红黑树节点
};

并且假设我们现在有一个struct rb_node* node指针,我们使用如下语句就能获取到该结构体：

1
struct person *p = container_of(node, struct person, rb);

此外还有一些比较常用的函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
// lib/rbtree.c  
  struct rb_node *rb_first(struct rb_root *tree);
  struct rb_node *rb_last(struct rb_root *tree);
  struct rb_node *rb_next(struct rb_node *node);
  struct rb_node *rb_prev(struct rb_node *node);

struct rb_node *rb_first(const struct rb_root *root)
{
	struct rb_node	*n;

	n = root->rb_node;
	if (!n)
		return NULL;
	while (n->rb_left) // 一直取最左边的结点
		n = n->rb_left;
	return n;
} 
EXPORT_SYMBOL(rb_first);

struct rb_node *rb_last(const struct rb_root *root)
{
	struct rb_node	*n;

	n = root->rb_node;
	if (!n)
		return NULL;
	while (n->rb_right)	// 一直取最右边的结点
		n = n->rb_right;
	return n;
}
EXPORT_SYMBOL(rb_last);

struct rb_node *rb_next(const struct rb_node *node)
{
	struct rb_node *parent;

	if (RB_EMPTY_NODE(node)) // 判断当前node的parent是不是指向自己，如果是说明该node没有被插入rb_root中，所以返回NULL。
		return NULL;

	/*
	 * If we have a right-hand child, go down and then left as far
	 * as we can.  如果有右子树，则取右子树的最左结点
	 */
	if (node->rb_right) {
		node = node->rb_right;
		while (node->rb_left)
			node = node->rb_left;
		return (struct rb_node *)node;
	}

	/*
	 * No right-hand children. Everything down and left is smaller than us,
	 * so any 'next' node must be in the general direction of our parent.
	 * Go up the tree; any time the ancestor is a right-hand child of its
	 * parent, keep going up. First time it's a left-hand child of its
	 * parent, said parent is our 'next' node.  如果没有右子树，则一直递归往上取。不过这里有个疑问，如果本身是最后一个结点了，那最后一个结点的最后一个结点是什么？
	 */
	while ((parent = rb_parent(node)) && node == parent->rb_right)
		node = parent;

	return parent;
}
EXPORT_SYMBOL(rb_next);

struct rb_node *rb_prev(const struct rb_node *node)
{
	struct rb_node *parent;

	if (RB_EMPTY_NODE(node))
		return NULL;

	/*
	 * If we have a left-hand child, go down and then right as far
	 * as we can.
	 */
	if (node->rb_left) {
		node = node->rb_left;
		while (node->rb_right)
			node = node->rb_right;
		return (struct rb_node *)node;
	}

	/*
	 * No left-hand children. Go up till we find an ancestor which
	 * is a right-hand child of its parent.
	 */
	while ((parent = rb_parent(node)) && node == parent->rb_left)
		node = parent;

	return parent;
}
EXPORT_SYMBOL(rb_prev);

增删改查

我们最为关心的增删改查。

在rb_tree中增加一个node

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// include/linux/rbtree.h
/**
 * rb_add() - insert @node into @tree
 * @node: node to insert
 * @tree: tree to insert @node into
 * @less: operator defining the (partial) node order
 */
static __always_inline void
rb_add(struct rb_node *node, struct rb_root *tree,
       bool (*less)(struct rb_node *, const struct rb_node *))
{
	struct rb_node **link = &tree->rb_node;
	struct rb_node *parent = NULL;

	while (*link) {
		parent = *link;
		if (less(node, parent))
			link = &parent->rb_left;
		else
			link = &parent->rb_right;
	} //这里先找到对应parent和link，即node要插入的位置的parent。

    //下面两个函数才是增加结点和平衡的关键
	rb_link_node(node, parent, link);
	rb_insert_color(node, tree);
}

我们先来看看rb_link_node函数。其实就是把link的值改成node。原本link是null。

1
2
3
4
5
6
7
8
9
//  include/linux/rbtree.h
static inline void rb_link_node(struct rb_node *node, struct rb_node *parent,
				struct rb_node **rb_link)
{
	node->__rb_parent_color = (unsigned long)parent;
	node->rb_left = node->rb_right = NULL;

	*rb_link = node;
}

然后是rb_insert_color函数, 内核代码里都写了很好的注释。其中很关键的点都画图了，这里注释小写证明红色（n, p, g, u），大写证明黑色(N,P,G,U)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
//  lib/rbtree.c
void rb_insert_color(struct rb_node *node, struct rb_root *root)
{
	__rb_insert(node, root, dummy_rotate);
}
EXPORT_SYMBOL(rb_insert_color);

static inline void dummy_rotate(struct rb_node *old, struct rb_node *new) {}

static inline struct rb_node *rb_red_parent(struct rb_node *red)
{
	return (struct rb_node *)red->__rb_parent_color;
}

static __always_inline void
__rb_insert(struct rb_node *node, struct rb_root *root,
	    void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
{
	struct rb_node *parent = rb_red_parent(node), *gparent, *tmp; //插入的结点必定是红色的

	while (true) {
		/*
		 * Loop invariant: node is red.
		 */
		if (unlikely(!parent)) {
			/*
			 * The inserted node is root. Either this is the
			 * first node, or we recursed at Case 1 below and
			 * are no longer violating 4). 如果插入的结点就是root，就把当前结点设置成黑色，又由于是root，也就是没有父结点，所以父结点是NULL。
			 * static inline void rb_set_parent_color(struct rb_node *rb,
			 *        struct rb_node *p, int color)
             *  {
             *      rb->__rb_parent_color = (unsigned long)p + color;
             *  }
			 */
			rb_set_parent_color(node, NULL, RB_BLACK);
			break;
		}

		/*
		 * If there is a black parent, we are done.
		 * Otherwise, take some corrective action as,
		 * per 4), we don't want a red root or two
		 * consecutive red nodes.  如果父亲是黑色，那么直接插入即可，因为不会打破平衡。
		 */
		if(rb_is_black(parent))
			break;

		gparent = rb_red_parent(parent);  //获取父亲的父亲 grandparent

		tmp = gparent->rb_right;  //尝试获取uncle结点。
		if (parent != tmp) {	/* parent == gparent->rb_left */ //说明是左子树， uncle是g的右子树
			if (tmp && rb_is_red(tmp)) { //其实就是从底部往上，因为当前结点是红的，并且uncle是红的，把parent和uncle都变成黑的，再把grandparent变成红的，然后往上递归。
				/*
				 * Case 1 - node's uncle is red (color flips).
				 *
				 *       G            g
				 *      / \          / \
				 *     p   u  -->   P   U
				 *    /            /
				 *   n            n
				 *
				 * However, since g's parent might be red, and
				 * 4) does not allow this, we need to recurse
				 * at g.
				 */
				rb_set_parent_color(tmp, gparent, RB_BLACK);
				rb_set_parent_color(parent, gparent, RB_BLACK);
				node = gparent;
				parent = rb_parent(node);
				rb_set_parent_color(node, parent, RB_RED);
				continue;
			}

			tmp = parent->rb_right; 
			if (node == tmp) {
				/* 说明当前node就是parent的右子树，就旋转
				 * Case 2 - node's uncle is black and node is
				 * the parent's right child (left rotate at parent).
				 *
				 *      G             G
				 *     / \           / \
				 *    p   U  -->    n   U
				 *     \           /
				 *      n         p
				 *
				 * This still leaves us in violation of 4), the
				 * continuation into Case 3 will fix that.
				 */
				tmp = node->rb_left;
				WRITE_ONCE(parent->rb_right, tmp);
				WRITE_ONCE(node->rb_left, parent);
				if (tmp)
					rb_set_parent_color(tmp, parent,
							    RB_BLACK);
				rb_set_parent_color(parent, node, RB_RED);
				augment_rotate(parent, node);
				parent = node;
				tmp = node->rb_right;
			}

			/*
			 * Case 3 - node's uncle is black and node is
			 * the parent's left child (right rotate at gparent).
			 *
			 *        G           P
			 *       / \         / \
			 *      p   U  -->  n   g
			 *     /                 \
			 *    n                   U
			 */
			WRITE_ONCE(gparent->rb_left, tmp); /* == parent->rb_right */
			WRITE_ONCE(parent->rb_right, gparent);
			if (tmp)
				rb_set_parent_color(tmp, gparent, RB_BLACK);
			__rb_rotate_set_parents(gparent, parent, root, RB_RED);
			augment_rotate(gparent, parent);
			break;
		} else {
			tmp = gparent->rb_left;
			if (tmp && rb_is_red(tmp)) {
				/* Case 1 - color flips */
				rb_set_parent_color(tmp, gparent, RB_BLACK);
				rb_set_parent_color(parent, gparent, RB_BLACK);
				node = gparent;
				parent = rb_parent(node);
				rb_set_parent_color(node, parent, RB_RED);
				continue;
			}

			tmp = parent->rb_left;
			if (node == tmp) {
				/* Case 2 - right rotate at parent */
				tmp = node->rb_right;
				WRITE_ONCE(parent->rb_left, tmp);
				WRITE_ONCE(node->rb_right, parent);
				if (tmp)
					rb_set_parent_color(tmp, parent,
							    RB_BLACK);
				rb_set_parent_color(parent, node, RB_RED);
				augment_rotate(parent, node);
				parent = node;
				tmp = node->rb_left;
			}

			/* Case 3 - left rotate at gparent */
			WRITE_ONCE(gparent->rb_right, tmp); /* == parent->rb_left */
			WRITE_ONCE(parent->rb_left, gparent);
			if (tmp)
				rb_set_parent_color(tmp, gparent, RB_BLACK);
			__rb_rotate_set_parents(gparent, parent, root, RB_RED);
			augment_rotate(gparent, parent);
			break;
		}
	}
}

这里看着代码比较复杂，其实就是利用递归来做旋转和变色，具体如下：

场景1：红黑树为空树

直接把插入结点作为根节点就可以了

另外：根据红黑树性质 2根节点是黑色的。还需要把插入节点设置为黑色

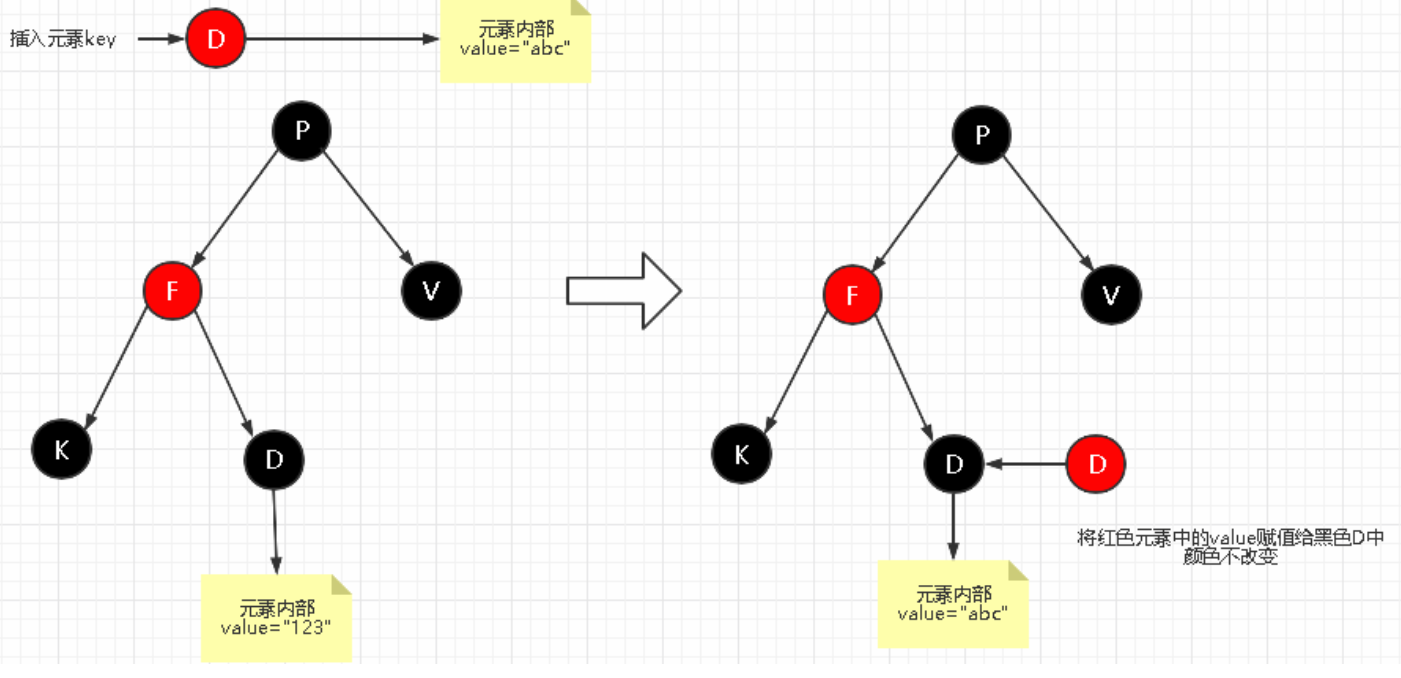
场景2：插入节点的Key已经存在

更新当前节点的值，为插入节点的值。

image-20250930190317643

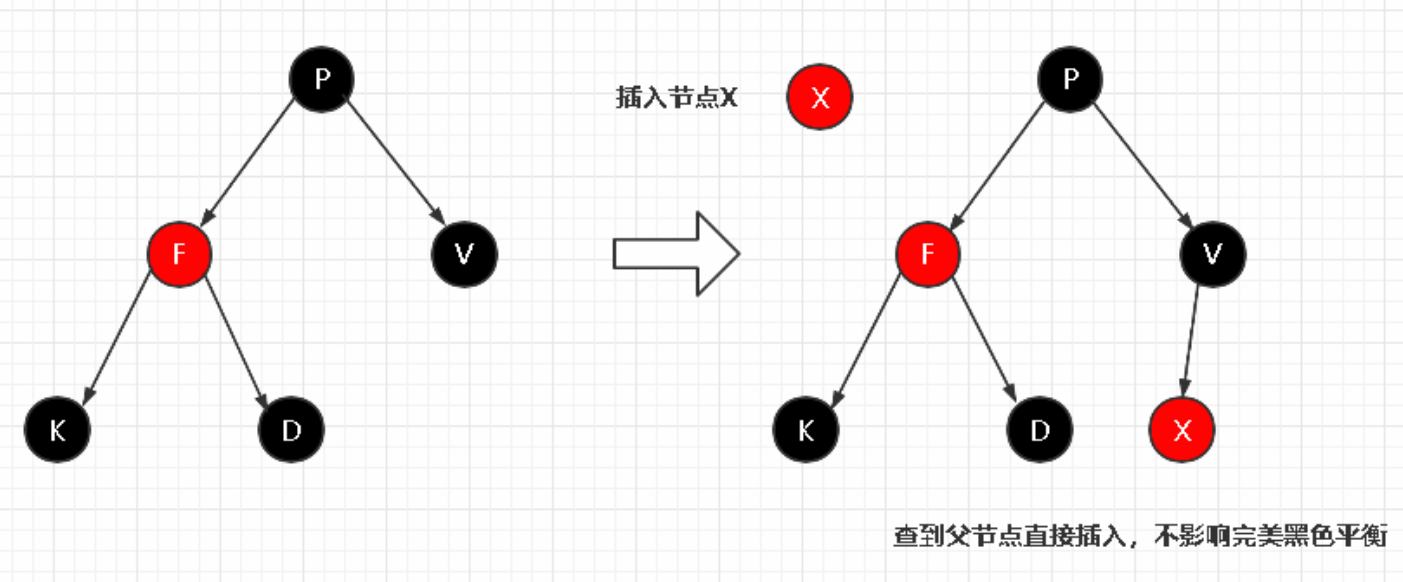
情景3：插入节点的父节点为黑色

由于插入的节点是红色的，当插入节点的父节点是黑色时，不会影响红黑树的平衡，

所以： 直接插入无需做自平衡。

image-20250930190359749

情景4：插入节点的父节点为红色

根据性质2：根节点是黑色。

如果插入节点的父节点为红色节点，那么该父节点不可能为根节点，所以插入节点总是存在祖父节点(三代关系)。

根据性质4：每个红色节点的两个子节点一定是黑色的。不能有两个红色节点相连。

此时会出现两种状态：

  • 父亲和叔叔为红色
  • 父亲为红色，叔叔为黑色

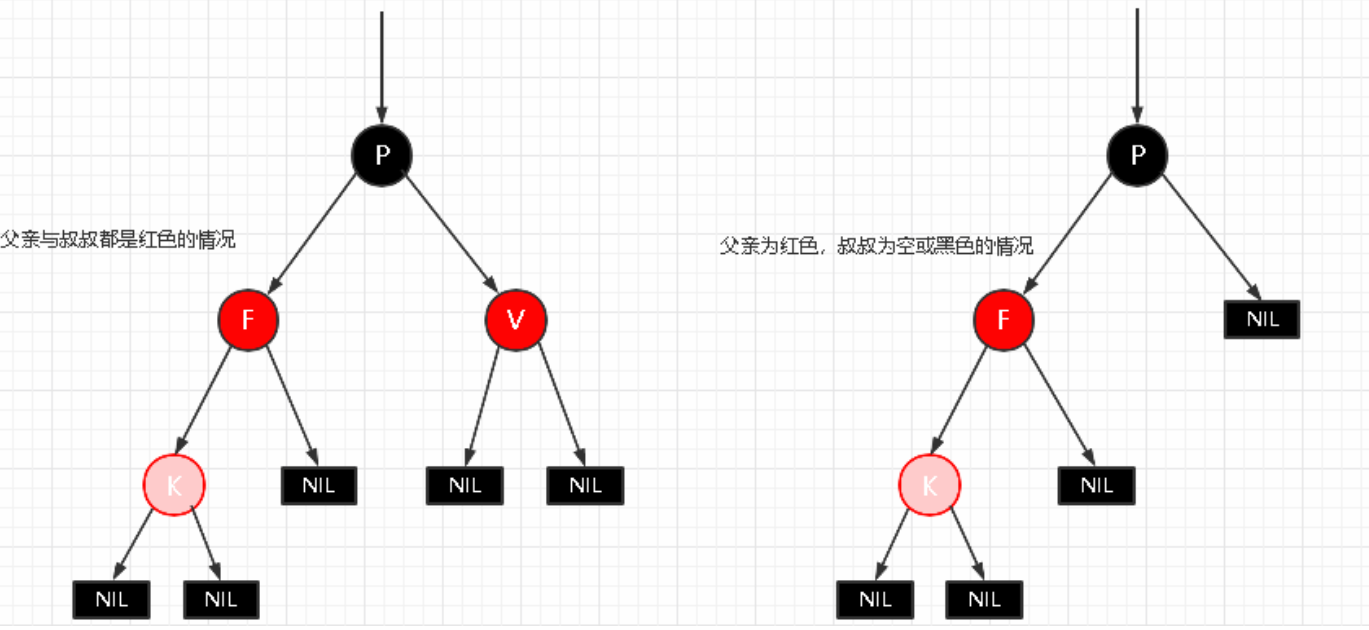
image-20250930190427233

场景4.1：父亲和叔叔为红色节点

根据性质4：红色节点不能相连 ==》祖父节点肯定为黑色节点：

父亲为红色，那么此时该插入子树的红黑树层数的情况是：黑红红。

因为不可能同时存在两个相连的红色节点，需要进行 变色， 显然处理方式是把其改为：红黑红

变色 处理：黑红红 ==> 红黑红

1.将F和V节点改为黑色

2.将P改为红色

3.将P设置为当前节点，进行后续处理

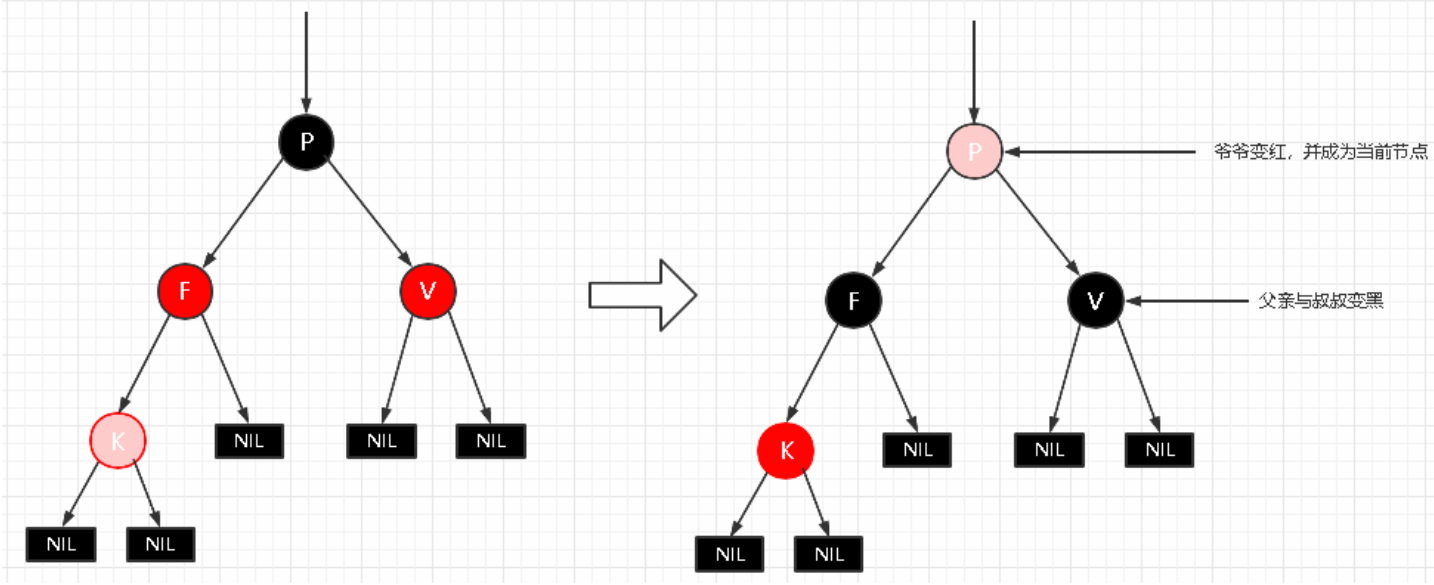
image-20250930190513948

将P设置为红色了，

如果P的父节点是黑色，那么无需做处理；

但如果P的父节点是红色，则违反红黑树性质了，所以需要将P设置为当前节点，继续插入操作, 作自平衡处理，直到整体平衡为止。

场景4.2：叔叔为黑色，父亲为红色，并且插在父亲的左节点

分为两种情况，当前结点是左节点和当前结点是右结点

  • 场景4.2.1 LL型失衡

把F设置成黑色，P设置成红色，然后右旋。

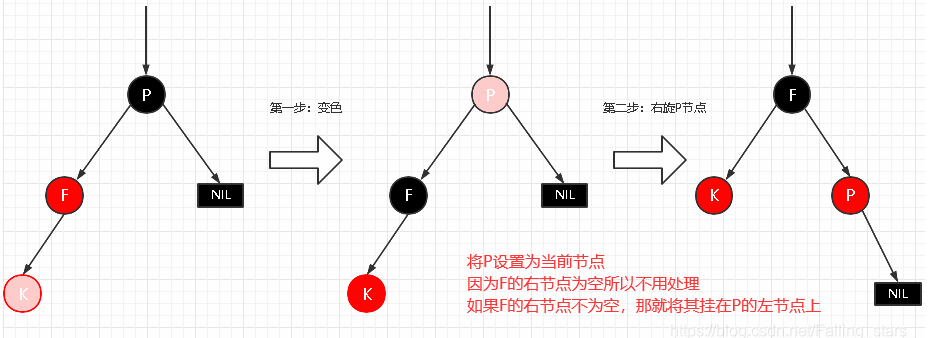
image-20250930190759084

  • 场景4.2.2 LR型失衡

把K和F进行左旋，转换成4.2.1

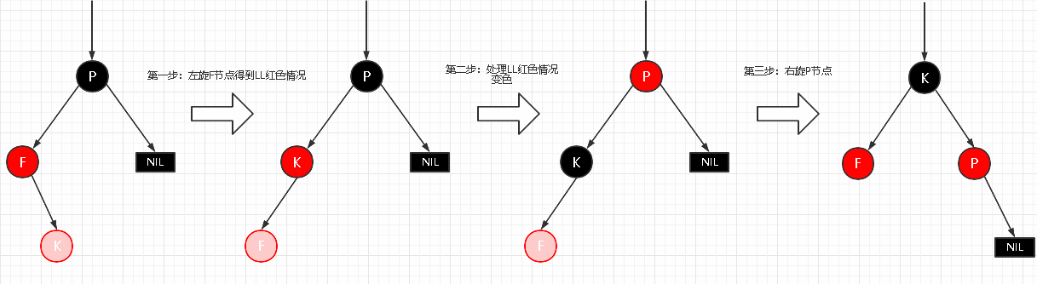
image-20250930190824711

同理RR失衡和RL失衡则不再重复。